---

0.背景

RNN模型，特别是包含着门控制的如LSTM等模型，近年来成了深度学习解决序列任务的标准结构。RNN层不但可以解决变长输入的问题，还能通过多层堆叠来增加网络的深度，提升表征能力和提升准确度。然而，标准的RNN（包括LSTM）受限于无法处理那些具有非常长的序列问题，例如文档分类或者字符级别的机器翻译；同样的，其也无法并行化的计算特征或者说，也无法同时针对文档不同部分状态进行计算。

CNN模型，特别适合处理图片数据，可是近年来也用在处理序列编码任务了(如文献1)。通过应用时间不变性的过滤器函数来并行的计算输入序列。CNN不同与循环模型的优点有：

• 增强并行化；
• 更好的处理更长的序列，如字符级别的语言数据。

而将CNN模型结合了RNN层生成的混合结构，能更好的处理序列数据（如文献2）。因为传统的最大池化和平均池化可以看成是：基于假设时间不变性前提下，在时间维度上结合卷积特征的一种方法。也就是说其本身是无法完全处理大规模序列有序信息的。

作者提出的Quasi RNN是结合了RNN和CNN的特性：

• 像CNN一样，基于时间步维度和minibatch维度上进行并行计算，确保对序列数据有高吞吐量和良好的长度缩放性；
• 像RNN一样，允许输出是依赖于序列中之前的有序元素基础上得到的，即RNN本身的过去时间依赖性

图0.1 LSTM，CNN，Quasi RNN结构图

如图0.1所示，其中就是通过结合LSTM和CNN的特性而构成的Quasi RNN。

1.Quasi RNN

Quasi RNN如CNN一样可以分解成2个子组件：

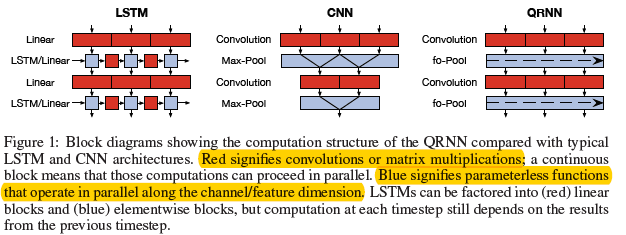
• 卷积组件：在序列数据上，基于序列维度并行计算（CNN是基于minibatch维度和空间维度），如图1.1.
• 池化组件：如CNN一样，该部分没有需要训练的参数，允许基于minibatch维度和特征维度上并行计算。

本人觉得图0.1略有些难以理解，自己画成如下图：

图1.1 基于序列数据的CNN卷积：假设\(t=3, k=2, x_i \in R^{n\times 1}, z_i \in R^{m\times 1}\)

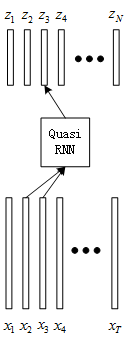
1. 假定输入为\(X\in R^{T\times n}\)，是一个长度为T的序列，其中每个向量维度为n。
2. QRNN如图1.1部分，假定卷积组件的通道是m（即滤波器个数是m），通过卷积操作得到\(Z\in R^{T\times m}\)，是一个长度为T的序列，其中每个向量维度为m。
3. 如果假定当前时间步为t，那么卷积的范围为\(x_{t-k+1}\)到\(x_t\)。

1.1. 卷积

然后就是Quasi RNN模块的内部结构了，其遵循如下公式：

$ Z = tanh(W_z * X) $ (1)

$ F = \sigma(W_f * X) $ (2)

$ O = \sigma(W_o * X) $ (3)

其中

\(W_z,W_f,W_o\)都是

\(R^{k\times n\times m}\)的张量，

\(*\)表示是以k为宽度的序列维度上的窗口滑动，如图1.1。假如

\(k=2\)，即卷积操作在序列维度上跨度为2，则上面式子如下所示：

$ z_t = tanh(W_z^1x_{t-1}+W_z^2x_t) $ (4)

$ f_t = \sigma(W_f^1x_{t-1}+W_f^2x_t) $ (5)

$ o_t = \sigma(W_o^1x_{t-1}+W_o^2x_t) $ (6)

如式子(4)(5)(6)所示，k的选取对于字符级别的任务还是很重要的。

1.2. 池化

在池化部分，作者建议了3种：

• f-pooling：动态平均池化,其中只用了一个遗忘门，\(\bigodot\)表示逐元素相乘
  \(h_t=f_t\bigodot h_{t-1}+(1-f_t)\bigodot z_t\) (7)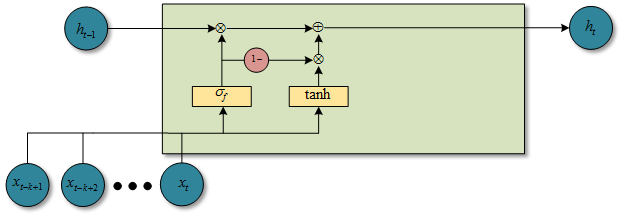
  
  图1.2.1 f-pooling时候的QRNN结构图
• fo-pooling：基于动态平均池化，增加一个输出门
  \(c_t=f_t\bigodot c_{t-1}+(1-f_t)\bigodot z_t\) (8)
  \(h_t = o_t\bigodot c_t\) (9)
  
  图1.2.2 fo-pooling时候的QRNN结构图
• ifo-pooling：具有一个独立的输入门和遗忘门
  \(c_t=f_t\bigodot c_{t-1}+i_t\bigodot z_t\) (10)
  \(h_t = o_t\bigodot c_t\) (11)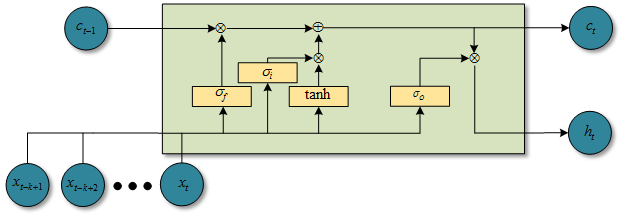
  
  图1.2.3 ifo-pooling时候的QRNN结构图

上述中\(h,c\)的状态都初始化为0，虽然对序列中每个时间步来说，这些函数的循环部分都需要计算，不过他们够简单，而且可以随着特征维度进行并行化。也就是对于实际操作中，对于即使很长的序列来说，增加的时间都是可以忽略不计的。一个QRNN层就是执行一个输入依赖的池化，后面跟着一个基于卷积特征和门控制的线性组合。正如CNN一样，随着QRNN层数增加，可以创建一个逼近更复杂函数的模型。

参考文献：

1. [CNN处理序列数据] - Xiang Zhang, Junbo Zhao, and Yann LeCun. Character-level convolutional networks for text classification.In NIPS, 2015.
2. [CNN+RNN] - Jason Lee, Kyunghyun Cho, and Thomas Hofmann. Fully character-level neural machine translation without explicit segmentation. arXiv preprint arXiv:1610.03017, 2016.